Resistividade
Também designada como Resistência Específica ou Resistividade Volumétrica define a oposição ao fluxo de eletrões através de um material.
Resistividade: Um condutor tem uma resistência que varia em função do material, da temperatura, do seu comprimento e da área da sua secção transversal. Assim, quanto menor a resistividade menor será a resistência elétrica do material.
Esta relação não é geral, é válida apenas para materiais uniformes e isotrópicos com secções transversais também uniformes. A temperatura influência a Resistência Específica dos materiais, normalmente os valores de resistividade são apresentados para temperaturas de 20ºC.
Em função da sua resistência elétrica, um determinado tipo de material pode ser considerado:
- Condutor: Material que conduz facilmente a corrente elétrica, denomina-se condutor. Pode ser metálico ou não metálico. Tem uma resistividade baixa. Estão incluídos nesta categoria o cobre, ouro, prata, alumínio etc.
- Isolador: Material que resiste fortemente ao fluxo da corrente, denomina-se isolador. Tem uma resistividade alta. Estão incluídos nesta categoria o vidro, madeira, plástico, borracha etc.
A medida da oposição de um material ao fluxo de corrente elétrica é dado pela seguinte formula:
ρ é a resistividade ou resistência específica (Ωm);
E é a amplitude do campo elétrico (V/m);
J é a densidade de corrente (A/m2)
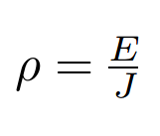
2ª Lei de Ohm ou Resistividade
Supondo que um material com 1m x 1m x 1m tem 1Ω de resistência, a sua resistividade será 1Ωm. Usar materiais com um metro quadrado de secção transversal para efetuar verificação não seria viável, por isso, faz-se a verificação da resistência elétrica com 1 metro de comprimento e 1mm2 de área na secção transversal e a sua representação será em (Ωmm2m), 1Ωm será igual a R(10-6m2/1m), no entanto, em muitos cálculos para evitar confusão na área da secção do material(condutor ou não), usa-se o Ωmm2m.
A resistência elétrica de um material pode ser calculado pela (2ª Lei de Ohm):
R: Resistência em Ω
S: Área da Secção Transversal em m2
ρ: Resistência especifica em Ωm
L: Comprimento em m(metro)
Como obter a área de um condutor circular?
A área (S) é calculada pela fórmula S=π r2
π=3.14151
r=raio
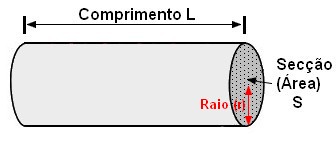
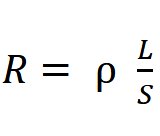
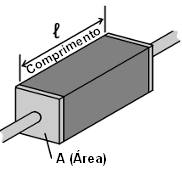
Comprimento: A resistência é tanto maior quanto maior for o comprimento.
Secção: A resistência é tanto menor quanto maior for o secção.
Resistência em função do tipo de material
Os materiais mais comuns têm os seguintes valores de resistividade.
| Material | Resistividade Ωmm2m |
|---|---|
| Prata | 0,016 |
| Cobre | 0,017 |
| Zinco | 0,061 |
| Alumínio | 0,030 |
| Ferro doce | 0,130 |
| Mercúrio | 0,950 |
| Carvão | 60 |
Resistência em função do tipo de material
Isoladores:
Têm uma resistividade entre 107 e 1023 Ωm.
Condutores:
Têm uma resistividade entre 10-8 e 10-6 Ωm.
Semicondutores:
A resistência diminui quando a temperatura aumenta.
Metais:
A resistência aumenta quando a temperatura aumenta.
Relação entre resistência e temperatura
A resistência elétrica de um condutor depende do tipo de material e da mobilidade
das partículas em seu interior. Na maior parte dos materiais o aumento da temperatura
significa maior resistência elétrica. Acontece porque, com o aumento da temperatura, existe um aumento
da agitação das partículas que constituem o material, aumentando as colisões entre as partículas e os eletrões livres no interior do condutor.
No caso metais e suas ligas é necessário um grande aumento na
temperatura para que se note uma variação mínima na resistência elétrica.
Conclui-se, então, que em um condutor, a variação na resistência elétrica relacionada ao aumento de
temperatura depende diretamente da variação de resistividade elétrica própria do material com o qual o
condutor é fabricado.
Assim, uma vez conhecida a resistividade do material do condutor a uma determinada temperatura, é
possível determinar seu novo valor em uma nova temperatura.
- ρf:(Ωmm2m) resistividade do material (temperatura final);
- ρ0:(Ωmm2m)resistividade do material (temperatura ambiente 20°C);
- α: coeficiente de temperatura do material (dado de tabela);
- ΔΘ: (°C)Variação de temperatura (temperatura final - temperatura inicial).
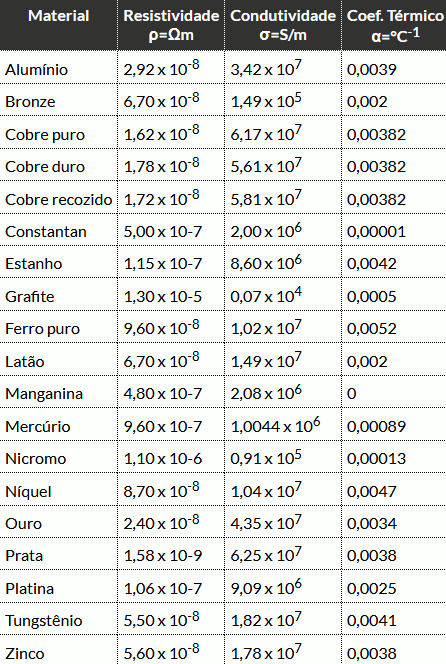
Resistividade, condutividade e coeficiente térmico dos principais condutores
A tabela seguinte mostra o valor do coeficiente de temperatura que corresponde à variação da resistência elétrica que o condutor do referido material, com resistência de 1 Ω, tem quando a temperatura varia 1°C.
Condutividade Elétrica
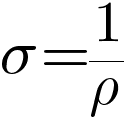
A Condutividade é recíproca à Resistividade, quanto mais elevado o valor da resistividade, menor será a condutividade.
- σ-Condutividade eléctrica em Siemens
- ρ-Resistividade em Ωm
Supercondutividade
A supercondutividade carateriza-se pela ausência de resistência elétrica, consegue-se obter a temperaturas próximas do zero absoluto(-273,15 °C). Em 2017, já se obteve materiais supercondutores a temperaturas muito acima do zero absoluto mas, mesmo assim, muito longe de temperaturas úteis de funcionamento. É, neste momento, o "Santo Graal" da física, conseguir "condutores" com resistência nula à temperatura ambiente, permitiria criar dispositivos a funcionar a elevadíssimas velocidades e com perdas muito reduzidas.
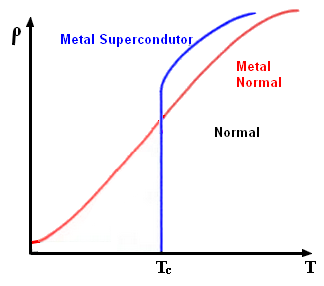
Quando a temperatura é menor que Tc, nos supercondutores, não existe resistência, a resistividade é zero. Nos condutores convencionais, embora a resistência baixe com a temperatura, nunca é zero.
Exemplos:
A resistividade é muito útil para o calculo das perdas nos fios condutores.
1.
Qual a resistência de um fio condutor em cobre com 200 metros e 1 mm2 de área na secção?
R = ρ L/S
R= 0,017 * 200 / 1 = 3,4
a resistência é igual a 3,4Ω
2.Um fio condutor de cobre unifilar tem 1 Km de comprimento e um raio de 2cm, qual a resistência aproximada do condutor?
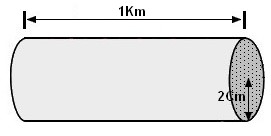
-Primeiro calculamos a área(secção)do condutor, S=π r2, convertemos para mm2, S=3.1415 x 202= 1256,6mm2.
-Como usamos a área em mm2, convertemos a resistividade do cobre para Ωmm2m e o comprimento em Km para metros.
-O cobre tem uma resistividade de 0,017Ωmm2m.
-O valor R = ρ L/S será R=0,017 x 1000 / 1256,6 = 0,0135 Ω.
Nota1: Para efeitos de cálculo, uma vez que a área dos condutores já está, normalmente, em mm2 usar os valores de resistividade em (Ωmm2m).
Nota2: Para converter Ωm em Ωmm2m, multiplica-se Ωm por 1000000 que é a razão da conversão(1m2 para mm2). A resistividade do Cobre 1,7 x 10-8=0,000000017 Ωm = 0,017 Ωmm2m. Erros nesta conversão geram muitos erros práticos.
Referências:
1. Electrical Installation Work, Level - pp.103 Peter Roberts,Mark Baker 2015.
2. Resistividade, condutividade e coef. térmico dos condutores - elaborada por Prof. Carlos Viana, 1°. Ano Engenharia FAENG.
3. Circuitos elétricos pp. 26 - Robert A. Bartkowiak, Universidade do Estado da Pensilvânia, 1995.
