Portas Lógicas - Electrónica Digital
Circuitos Digitais - Portas Lógicas
Circuitos lógicos ou portas lógicas, são dispositivos que, em função de um ou mais sinais lógicos de entrada ("0" ou "1") , produzem uma e apenas uma saída.
O Circuito Digital opera em dois Níveis de Tensão diferentes, Baixo e Alto. Geralmente, o Nível Baixo corresponde ao valor Lógico 0 e o Nível Alto corresponde ao valor Lógico 1. As Portas Lógicas são blocos de construção básicos na Electrónica Digital. A relação entre a(s) Entrada(s) e a Saída de uma Porta Lógica pode ser exprimida numa Tabela de Verdade.
A saída em função da(s) entrada(s) é definido pela lógica de Boole.
As portas são desenvolvidas dentro de circuitos integrados que podem ter várias portas ou, em alguns, funções especificas dadas pela funcionamento conjunto de diferentes portas.
Existem CI de diferentes tecnologias (MOS, TTL etc...) que fazem com que exista alguma diferença no valor ALTO e BAIXO tanto de entrada como de saída.
Inversor, Porta NÃO (NOT Gate) e Seguidor (Buffer)
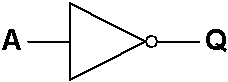
Um Inversor é uma Porta Lógica que tenha apenas uma Entrada. A sua Saída é o Estado Lógico complementar da sua Entrada. O Inversor é também designado como a Porta NÃO. O Símbolo Esquemático de um Inversor básico é mostrado na Figura 1 e a Tabela 1 é a sua Tabela de Verdade.
A notação da operação lógica de um Inversor pode ser expressa por:
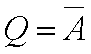
| A | Q |
|---|---|
| 0 | 1 |
| 1 | 0 |
Tabela 1: Tabela de Verdade do Inversor
Seguidor
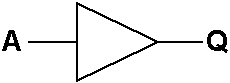
Um Seguidor é outra Porta Lógica com apenas uma Entrada, e a sua Saída segue o mesmo Estado Lógico da sua Entrada. O Seguidor é utilizado como um elemento de atraso na Electrónica Digital. É também um elemento para Esforçar a Corrente, que aumenta a capacidade de Saída de forma a conduzir outras portas. O Símbolo Esquemático de um Seguidor é mostrado na Figura 2 e a Tabela 2 é a sua Tabela de Verdade.
A notação da operação lógica de um Seguidor pode ser expressa por:
![]()
| A | Q |
|---|---|
| 0 | 0 |
| 1 | 1 |
Tabela 2: Tabela de Verdade do Seguidor
Portas E (AND)
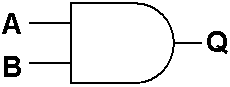
Uma Porta E é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 1 se e só se todas as suas Entradas são 1. O Símbolo Esquemático de uma Porta E com Duas Entradas é mostrado na Figura 3 e a Tabela 3 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta E pode ser expressa por:
![]()
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tabela 3: Tabela de Verdade de uma Porta E (AND)
Portas NÃO E (NAND)
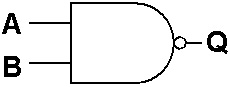
Uma Porta NÃO E é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 0 se e só se todas as suas Entradas são 1. O Símbolo Esquemático de uma Porta NÃO E com Duas Entradas é mostrado na Figura 4 e a Tabela 4 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta NÃO E pode ser expressa por:
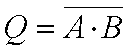
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
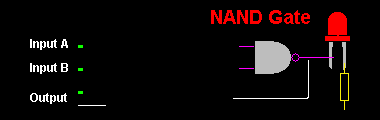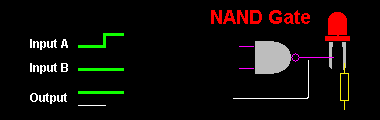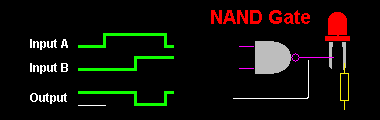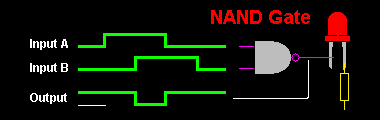
Tabela 4: Tabela de Verdade de uma Porta NÃO E (NAND)
Portas OU (OR)
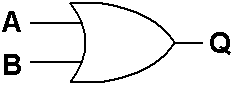
Uma Porta OU é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 0 se e só se todas as suas Entradas são 0. O Símbolo Esquemático de uma Porta OU com Duas Entradas é mostrado na Figura 5 e a Tabela 5 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta OU pode ser expressa por:
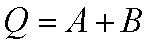
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Tabela 5: Tabela de Verdade de uma Porta OU (OR)
Portas NÃO OU (NOR)
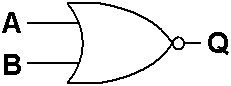
Uma Porta NÃO OU é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 1 se e só se todas as suas Entradas são 0. O Símbolo Esquemático de uma Porta NÃO OU com Duas Entradas é mostrado na Figura 6 e a Tabela 6 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta NÃO OU pode ser expressa por:
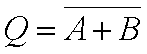
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |

Tabela 6: Tabela de Verdade de uma Porta NÃO OU (NOR)
Portas OU Exclusivo (XOR)
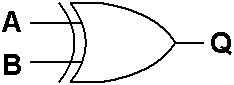
Uma Porta OU EXCLUSIVO é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 1 se e só se apenas uma das suas Entradas é 1. O Símbolo Esquemático de uma Porta OU EXCLUSIVO com Duas Entradas é mostrado na Figura 1 e a Tabela 1 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta OU EXCLUSIVO pode ser expressa por:
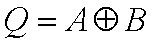
| A | B | Q |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tabela 8: Tabela de Verdade de uma Porta OU EXCLUSIVO
Portas NÃO OU Exclusivo (XNOR)
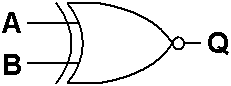
Uma Porta NÃO OU EXCLUSIVO é uma Porta Lógica que tem duas ou mais Entradas. A sua Saída é 1 se e só se todas as Entradas estão no mesmo Estado Lógico. O Símbolo Esquemático de uma Porta NÃO OU EXCLUSIVO com Duas Entradas é mostrado na Figura 2 e a Tabela 2 é a sua Tabela de Verdade.
A notação da operação lógica de uma Porta NÃO OU EXCLUSIVO pode ser expressa por:
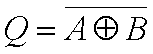
| A | B | Q |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tabela 9: Tabela de Verdade de uma Porta NÃO OU EXCLUSIVO
Semi – Somador e Somador Completo Básico (de 1 bit)
Em electrónica, um Somador é um dispositivo que faz a adição entre dois números.
Um Semi-Somador é um Circuito Lógico que realiza a adição binária de 1 bit. Dado dois números binários de 1 bit, P e Q, S é a Soma de 1 bit entre P e Q, e ST é o bit da SAÍDA DE TRANSPORTE. Matematicamente, S e ST formam uma Soma Aritmética de 2 bits entre P e Q, Figura 3. ST é o Bit Mais Significativo (BMS). A Figura 4 mostra todos os casos possíveis para a adição binária de 1 bit. A Tabela 3 é a Tabela de Verdade do Semi-Somador.
| 1 | ←P | ||
| +) | 1 | ←Q | |
|
|
|||
| 1 | 0 | ||
| ↑ | ↑ | ||
| ST | S | ||
Figura 3: Adição de dois números binários de 1 bit
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 0 com o Transporte de 1 |
Figura 4: Todos os casos possíveis para a adição binária de 1 bit
| Entradas | Saídas | ||
|---|---|---|---|
| P | Q | CO | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Tabela 3: Tabela de Verdade do Semi-Somador
Analisando a Tabela de Verdade e considerando a relação lógica entre as Entradas e as Saídas de um Semi-Somador, S é o resultado da operação OU EXCLUSIVO das Entradas e ST é o resultado da operação E das Entradas. Isto significa que o circuito Semi-Somador pode ser implementado somente com duas Portas Lógicas: uma Porta OU EXCLUSIVO e uma Porta E, Figura 5.
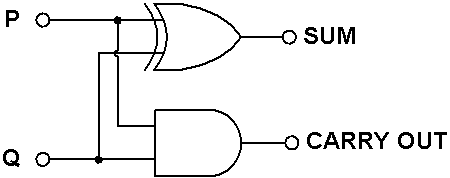
Figura 5: Semi-Somador
O Semi-Somador só pode realizar a adição de dois números binários com 1 bit cada, uma vez que não aceita a ENTRADA DE TRANSPORTE (ET), proveniente da adição prévia de dois bits, conforme permite o circuito inferior.
Um Somador Básico Completo é um Circuito Lógico que faz a adição entre dois números de 1 bit com o bit de transporte, ET. O Somador Completo consiste em uma Porta OU e dois Semi-Somadores, Figura 6. O circuito gera duas Saídas: S e ST. Múltiplos Somadores Completos podem fluir para formar um Somador Completo de Múltiplos Bits.
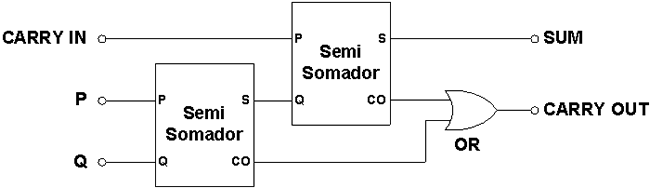
Figura 6: Somador Básico Completo
Somador Completo (4 bit)
Combinando vários Somadores Completos Básicos (de 1 bit) em cascata, é possível construir um Somador Completo de Múltiplos Bits. Na Figura 7, um Somador Progressivo de 4 bits é construído pela ligação de quatro Somadores Completos Básicos. O bit SAÍDA DE TRANSPORTE, ST (CO), do Somador Completo Básico está ligado à ENTRADA DE TRANSPORTE, ET (CI), do Somador Completo Básico seguinte mais significativo .
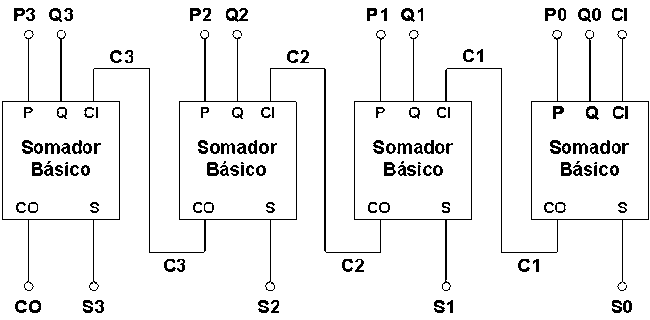
Figura 1: Somador de Transporte Progressivo de 4 bits construído com quatro Somadores Completos Básicos
A adição de dois Números Binários de Múltiplos Bits P e Q faz-se adicionando os bits sucessivamente, começando por somar os Bits menos Significativos BmS, isto é, P0 + Q0. Qualquer bit de Transporte, proveniente da soma de anteriores bits, é adicionado à soma dos próximos bits consecutivos, Figura 8.
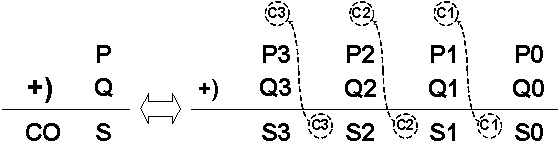
Figura 8: Adição de dois Números Binários de 4 bits, com exemplificação da operação de Transporte
Para um Número Binário P de 5 bits, os pesos dos bits mais significativos são:
| P0 = 20 = 1 |
| P1 = 21 = 2 |
| P2 = 22 = 4 |
| P3 = 23 = 8 |
| P4 = 24 = 16 |
A fórmula para converter um Número Binário de 5 bits P2 (P4 P3 P2 P1 P0) no seu correspondente Número Decimal P10 é:
P10 = P4 x 24 + P3 x 23 + P2 x 22 + P1 x 21 + P0 x 20
O bit ST (CO) de um Somador Completo de 4 bits é equivalente ao quarto bit mais significativo e o seu peso é de 16 (24 = 16).
O maior número decimal que pode ser obtido de um Somador Completo de 4 bits é 31 (24+1 – 1 = 31).
Circuitos Práticos de Testes de portas lógicas
Os circuito digitais testados vão usar tecnologia CMOS, por esse motivo os circuitos integrados permitem uma variação maior de tensão com um consumo mais reduzido. Os circuitos CMOS são susceptíveis de ficarem danificados com electricidade estática, tome as precauções adequadas se pretende testar estes circuitos.
Circuitos usando tecnologia TTL têm de ter uma fonte de alimentação com 5V, não toleram uma variação significativa destes valores.
Para os testes práticos vamos usar uma placa de testes.
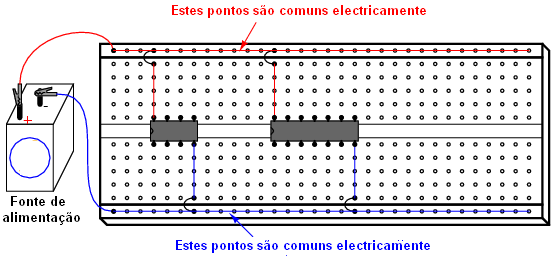
Funções básicas das portas lógicas
Componentes e materiais
- 4011 quad NAND gate
- Eight-position DIP switch
- Ten-segment bargraph LED - Normalmente os leds usados nos vuímetros
- Bateria ou Fonte de alimentação de 6V
- Duas resistências 10 kΩ
- Três resistências 470 Ω
Atenção! O 4011 IC é CMOS, é por isso sensível a descargas electricas estáticas!
