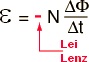Lei faraday

Segundo a lei de Faraday, se o fluxo do campo magnético (Φ)através da superfície limitada por um circuito varia com o tempo (Δt), aparece nesse circuito uma força eletromotriz (ε) induzida.
Matematicamente:

ε = - ΔΦ / Δt



Onde:
ε = Fem = Força eletromotriz (Tensão gerada ou induzida).
Φ = BA = Fluxo magnético
N = Número de espiras
B = Campo magnético externo
A = Área da bobina
t = Tempo.

Verificação Prática Lei de Faraday

Movimento Bobina em Campo Magnético

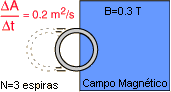
ε = -3 x 0,3T x 0,2 m² = -0,18 volt

Movimento Íman na Bobina

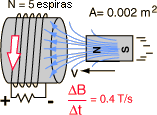
ε = -5 x 0,002m² x 0,4T/s = -0,004 volt

Alterando o Fluxo Magnético

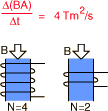
ε = -4 x 4 = -16 volt (N=4 espiras)
ε = -4 x 2 = -8 volt (N=2 espiras)

Rotação Bobina em Campo Magnético

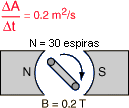
ε = -30 x 0,2T x 0,2m² = -1,2 volt

Verificação Prática Lei de Faraday

O objetivo é verificar a lei de Faraday aproximando e afastando um ímã duma espira ligada a um amperímetro (Fig. 1) e variando a corrente numa espira próxima a outra espira, essa ligada a um amperímetro (Fig. 2).

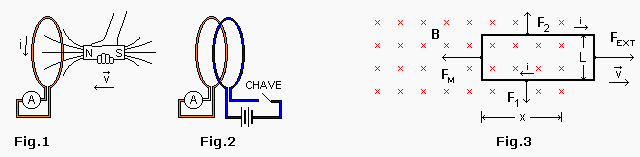
Como exemplo de aplicação da lei de Faraday vamos calcular a fem induzida numa espira retangular que se movimenta entrando ou saindo, com velocidade constante, de uma região de campo magnético uniforme (Fig.3). O fluxo do campo magnético através da superfície limitada pela espira vale ε =xLB e a sua variação no tempo Δ Φ/ Δt = (Δx/ Δt)LB = vLB. Assim:

ε = vLB
e se a espira tem uma resistência R, a corrente induzida é:

i = ε/ R = vLB / R

Um condutor percorrido por uma corrente elétrica mergulhado num campo magnético fica sob a acção de uma força dada por F = i L x B. Assim, por efeito da corrente induzida na espira, aparecem as forças F₁, F₂ e F_M. As duas primeiras anulam-se mutuamente. A terceira é cancelada por uma força externa, necessária para manter a espira com velocidade constante. Como a força F_M deve se opor à força F_EXT, a corrente induzida na espira pela variação do fluxo magnético deve ter o sentido indicado na Fig.3. Esse fato constitui um exemplo particular da lei de Lenz.